Introduction
This model aims to predict the outcome of the Electoral College, thereby determining the next President of the United States. Consequently, I chose not to predict the national vote share, as it is not irrelevant to the outcome of the election.
As an aside, I strongly believe the Electoral College should be abolished. If you’re interested in exploring an innovative proposal on this topic, please read this article I wrote for the Harvard Political Review.
This model is based on the assumption that only the following states are truly competitive: Arizona, Georgia, Michigan, Nevada, North Carolina, Pennsylvania, and Wisconsin. I identified these states as battlegrounds in my Week #1 Post, an assessment shared by other experts such as the Cook Political Report. Therefore, this model will focus exclusively on predicting the two-party vote share in these seven states, assuming an initial distribution of electoral votes where Harris holds 226 and Trump holds 219.
Given the volume of polls that only display these states as toss-ups, I am confident in this assumption. However, a recent poll by Selzer & Co.—a highly respected pollster—found Harris leading by 3 points in Iowa, a state Trump won by 8 points in 2020. If accurate, this poll could challenge the model’s assumptions and potentially signal a landslide Harris electoral college victory, exceeding the model’s maximum of 319 electoral votes.
Model Equations
For this model, I wanted to balance the effects of fundamentals and polling based on historical election outcomes to increase the predictive accuracy of my model. Given this, I chose to use a super-learning model ensembling method predicting the expected vote share with three distinct Ordinary Least Square (OLS) models and then combining them using empirically generated weights.
Initially, I had created one set of weights I had used for all the swing states, but I soon realized that having individual weights for each state would lead to lower RMSE. As a result, I chose to loop the swing states and create separate models using Florida as an intercept. Since I created three individual models for each state or 21 models in total, I chose not to include the summaries of the coefficients.
I used data from the 1980 - 2020 elections to train the models, the largest range where all data was available.
Model 1:
$$ `\begin{aligned} D\_pv2p = & \, \alpha + \beta_1(\text{state}) + \beta_2(\text{D\_pv2p\_lag1}) + \beta_3(\text{D\_pv2p\_lag2}) \\ & + \beta_4(\text{updated\_rdpi} \times \text{incumbent\_party}) + \beta_5(\text{dpi\_inflation\_adjusted} \times \text{incumbent\_party}) + \epsilon \end{aligned}` $$The first model uses only fundamental predictors, including lagged Democratic two-party vote shares from 2016 and 2020 and two measures of Real Disposable Personal Income (RDPI).
The first RDPI measure, “updated RDPI,” is the most recent national RDPI data available, covering June 1 to September 1 of the election year (between Q2 and Q3). This data is sourced from the Federal Reserve Bank of St. Louis. To avoid the economic impact of the COVID-19 pandemic on 2020 data, I used the Congressional Budget Office’s 2020 RDPI growth projections rather than actual values.
The second RDPI measure, “DPI inflation-adjusted,” uses state-level disposable income data from the Bureau of Economic Analysis, adjusted for inflation with World Bank data. Since quarterly state-level DPI is unavailable for 2024, I used data from the year preceding the election.
Both economic variables are modeled as interaction effects, with a binary variable indicating the incumbent party. Including both state and national predictors helps capture voter perceptions of national economic conditions and personal financial situations.
Model 2:
$$ `\begin{aligned} D\_pv2p = & \, \alpha + \beta_1(\text{state}) + \beta_2(\text{polling\_trend\_5\_1}) + \beta_3(\text{polling\_trend\_10\_6}) \\ & + \beta_4(\text{current\_week}) + \beta_5(\text{support\_DEM\_1}) + \beta_6(\text{support\_DEM\_2}) + \beta_7(\text{support\_DEM\_3}) + \epsilon \end{aligned}` $$The second model relies solely on various polling-based covariates, all sourced from FiveThirtyEight with their poll weighting applied. The data is state-level and grouped by the weeks remaining before the election.
The first three polling variables—Polling Trend 5-1, Polling Trend 6-10, and Current Week—are measured in poll margin (Democratic candidate polling minus Republican candidate polling). Polling Trend 5-1 captures the change in margin from five weeks to one week before the election, indicating whether a candidate is gaining or losing ground close to Election Day. Polling Trend 6-10 reflects changes from six to ten weeks out, while Current Week is the margin from one week before the election.
The last three variables—Support Dem. 1, Support Dem. 2, and Support Dem. 3—represent the average Democratic candidate polling one, two, and three weeks before the election, respectively. I chose to include these covariates to capture additional shifts in Democratic candidate support as the election approaches.
Model 3:
$$ `\begin{aligned} D\_pv2p = & \, \alpha + \beta_1(\text{state}) + \beta_2(\text{D\_pv2p\_lag1}) + \beta_3(\text{D\_pv2p\_lag2}) + \beta_4(\text{support\_DEM\_1}) \\ & + \beta_5(\text{polling\_trend\_5\_1}) + \beta_6(\text{polling\_trend\_10\_6}) + \beta_7(\text{dpi\_inflation\_adjusted} \times \text{incumbent\_party}) \\ & + \beta_8(\text{unemployment\_growth\_quarterly} \times \text{incumbent\_party}) + \beta_9(\text{updated\_rdpi} \times \text{incumbent\_party}) + \epsilon \end{aligned}` $$The third model combines Models 1 and 2 covariates with the addition of national-level Q2 unemployment growth from the Fed. in St. Louis, which is included as an interaction effect with the incumbent party. Including this factor reduced the RMSE, which led me to incorporate it in this combined model.
Weights
To generate weights without excluding election cycles and reduce overfitting concerns from training on a single election, I used a Leave-One-Out scheme where I trained all three models, excluding one election cycle at a time, and then predicted the results for the excluded election.
After repeating this process for each election in the dataset, I performed a constrained optimization with a Beta between 0 and 1 using the three predicted values (each from one of the above models) and the actual vote share to generate the individual state weights. Table 1 below displays the resulting weights for each state.
| State | Weight.Model.1 | Weight.Model.2 | Weight.Model.3 |
|---|---|---|---|
| Arizona | 0.0281 | 0.9719 | 0.0000 |
| Georgia | 0.1304 | 0.8381 | 0.0315 |
| Michigan | 0.1293 | 0.6102 | 0.2604 |
| Nevada | 0.1276 | 0.7298 | 0.1426 |
| North Carolina | 0.3955 | 0.5703 | 0.0342 |
| Pennsylvania | 0.0312 | 0.9585 | 0.0104 |
| Wisconsin | 0.1537 | 0.6419 | 0.2043 |
The second model, which relies solely on polling data, consistently receives the highest weight. In states like Arizona and Pennsylvania, its weight comprises nearly the entire model, while in Michigan and Nevada, it is slightly above 0.5.
The fundamental model is weighted just above 0.1 in four swing states, reaching nearly 0.4 in North Carolina and dips to a low in Pennsylvania and Arizona. Model 3, the combined model, shows the greatest variance, with weights close to zero in some states and over 0.2 in others. Overall, the weights clearly vary significantly depending on the state.
RMSE (In-sample & Out-of-sample)
To test the predictive accuracy of this model, I calculated both in-sample and out-of-sample root mean square error (RMSE) based on the 2020 election. For the in-sample RMSE, I included 2020 data in the training set while using the same weights derived from all prior elections. For the out-of-sample RMSE, I excluded the 2020 data from the training set, but still applied the same weights. Although this means the out-of-sample RMSE reflects weights partially trained on 2020 data, removing this data would be challenging given the method I used for generating the weights, and the impact of any single election on weight determination is minimal.
The in-sample RMSE results, in Table 2, were encouraging, ranging from a low of 0.04 in Georgia to a high of 2.05 in Wisconsin, indicating that the maximum prediction error was within 2 percentage points—enough to potentially swing a state. Most of the error came from overestimating the Democratic vote share.
| State | RMSE.2020 | Predicted.Vote.Share | True.Vote.Share |
|---|---|---|---|
| Arizona | 0.6719 | 49.4850 | 50.1568 |
| Georgia | 0.0435 | 50.1629 | 50.1193 |
| Michigan | 1.5867 | 53.0003 | 51.4136 |
| Nevada | 1.5505 | 52.7736 | 51.2231 |
| North Carolina | 0.5768 | 48.7390 | 49.3158 |
| Pennsylvania | 1.7680 | 52.3572 | 50.5892 |
| Wisconsin | 2.0518 | 52.3709 | 50.3191 |
The out-of-sample RMSE results, while expectedly higher, remained strong. The highest RMSE was in Pennsylvania at 2.46, due to a significant overestimation of the Democratic vote share. This is likely due to the model’s reliance on polling data for Pennsylvania, as shown in Table 1, where polling errors led to an overestimate.
| State | RMSE.2020 | Predicted.Vote.Share | True.Vote.Share |
|---|---|---|---|
| Arizona | 0.3713 | 49.7855 | 50.1568 |
| Georgia | 0.2846 | 49.8347 | 50.1193 |
| Michigan | 1.1598 | 52.5734 | 51.4136 |
| Nevada | 1.2268 | 52.4499 | 51.2231 |
| North Carolina | 1.5875 | 47.7283 | 49.3158 |
| Pennsylvania | 2.4631 | 53.0523 | 50.5892 |
| Wisconsin | 1.9281 | 52.2472 | 50.3191 |
Ensemble Model Predictions
Now, with the preamble complete, we can finally reach the main event: Who will win the 2024 Presidential Election?
Using data from 2024, my model predicts that Harris will narrowly win in Pennsylvania and Wisconsin, with more substantial leads in Michigan and Nevada—enough to reach 270 electoral votes and become America’s 47th President. She is projected to lose Arizona by a large margin, with close losses in both North Carolina and Georgia, finishing with 276 electoral votes to Trump’s 262.
| State | Margin |
|---|---|
| Arizona | -4.41% |
| Georgia | -1.53% |
| Michigan | 2.82% |
| Nevada | 3.37% |
| North Carolina | -1.51% |
| Pennsylvania | 0.61% |
| Wisconsin | 1.38% |
You can view the margins in Table 4 above or by hovering over the states in the interactive map below .
Simulations
However, even if my model were 100% accurate, these predictions would only hold if polling error were zero. As we saw in 2016 and 2020, polling errors can be significant, sometimes even reversing expectations entirely, as in 2016.
To account for this, I ran 1,000 simulations of all polling-based covariates, using a normal distribution centered around the mean with a standard deviation of 3. I then predicted Harris’s total electoral vote share in all 1,000 simulations to estimate her likelihood of winning the election.
The plot below represents the distribution of these simulations, with each dot representing five simulations. Harris victories are shown in blue, while losses are shown in red. As you can see, the majority of simulations predict a Harris victory, with the most common outcome being Harris achieving 276 electoral votes, the scenario predicted above. As expected, the most common loss scenario is when Harris earns only 257 electoral votes, primarily from losing Pennsylvania.
Table 5 below shows that, out of the 1,000 simulations, Harris wins in 589 and loses in 411.
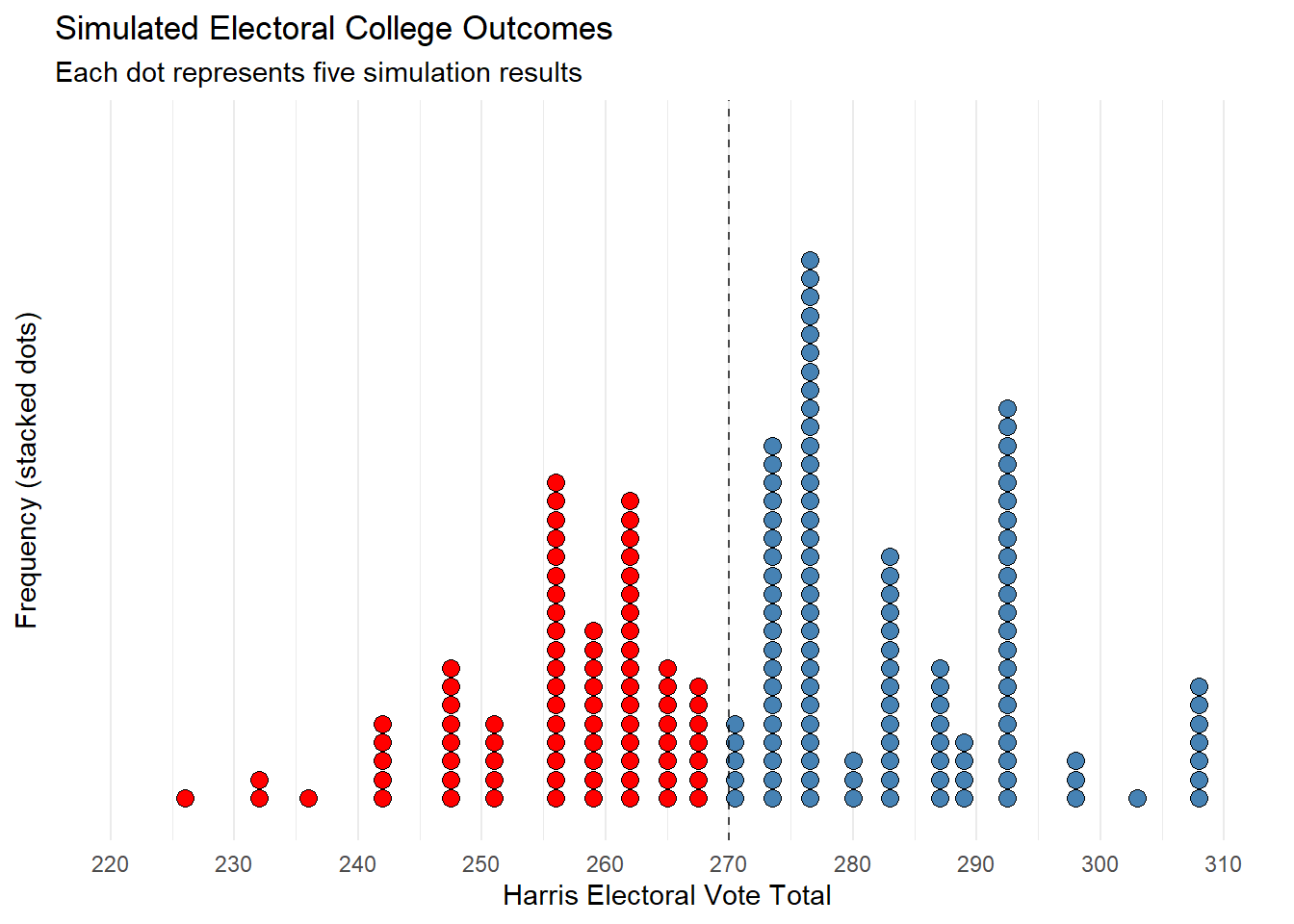
| Harris Victory Wins | Trump Victory Wins | Harris Victory % |
|---|---|---|
| 589 | 411 | 58.9% |
Conclusion & Acknowledgements
Overall, my model suggests that Harris has a slightly higher chance of winning the election, but ultimately, the race is still a toss-up and far too close to call.
In closing, I would like to acknowledge the exceptional faculty and course staff of Gov 1347: Election Analytics, without whose teaching and guidance this project would not have been possible: Professor Ryan Enos, Teaching Fellow Matthew Dardet, and Course Assistants Ethan Jasney and Yusuf Mian.
Thank you for reading, and I hope you enjoyed this analysis! If you have any questions or feedback, please feel free to reach out to me at aviagarwal@college.harvard.edu.